[1]:
%%capture
import os
import emzed
import matplotlib.pyplot as plt
data_folder = os.path.join(os.getcwd(), "tutorial_data")
aa_peaks_table = os.path.join(data_folder, "AA_peaks.table")
emzed provides a module chemistry emzed.chemistry, which features linking spectral and chemical information.
elements is a Table containing detailed information of 95 atoms and its isotopes.
[2]:
emzed.chemistry.elements[10:15]
[2]:
| atomic_number | symbol | name | average_mass | mass_number | mass | abundance |
|---|---|---|---|---|---|---|
| int | str | str | float | int | float | float |
| 5 | B | Bor | 10.8110277680 | 10 | 10.0129370000 | 0.199 |
| 5 | B | Bor | 10.8110277680 | 11 | 11.0093050000 | 0.801 |
| 6 | C | Carbon | 12.0107358985 | 12 | 12.0000000000 | 0.989 |
| 6 | C | Carbon | 12.0107358985 | 13 | 13.0033550000 | 0.011 |
| 7 | N | Nitrogen | 14.0067430888 | 14 | 14.0030740000 | 0.996 |
However, accessing information of an element via a table that lists all elements is a little cumbersome. In daily routine, isotopologue masses and isotopologue distributions are most required. We start with mass
[3]:
mass = emzed.mass
print(
f"""
carbon:\t{mass.C}
C12:\t{mass.C12}
C13:\t{mass.C13}
glucose:\t{mass.of('C6H12O6')}
U-13C glucose:\t{mass.of('[13]C6H12O6')}
1-13C glucose:\t{mass.of('[13]CC5H12O6')}"""
)
carbon: {12: 12.0, 13: 13.003355}
C12: 12.0
C13: 13.003355
glucose: 180.0633903828
U-13C glucose: 186.0835203828
1-13C glucose: 181.0667453828
Hence, mass provides isotope masses and features calculating masses of molecular formulas. If you do not precise the isotope mass returns a dictionary with all isotopes of the atom. The method mass.of calculates monoisotopic masses or the mass of the lightest isotope M0, respectively. To calculate the mass of a specific isotopologue you have to specify the isotope number in brackets prior to the element.
The exact isotopologue distribution of a compound can be calculated with the method compute_centroids .
compute_centroids(mf, explained_abundance, *, abundances=None)
with arguments:
mf: molecular formula as string i.e. ‘C6H12O6’
mf: explained_abundance: stopping criterium. The value ranges between 0 and 1. The higher the value the more accurate the result, the longer the calculation time.
abundance, allows user defined definition of elemental isotope distributions i.e. dict(C={12: 0.1, 12: 0.9})
It returns a Table listing possible isotope combinations and their abundance. Again, an example with glucose
[4]:
compute = emzed.chemistry.compute_centroids
mf = "C6H12O6"
compute(mf, 0.999)
[4]:
| id | mf | m0 | abundance |
|---|---|---|---|
| int | str | MzType | float |
| 0 | [12]C6 [1]H12 [16]O6 | 180.063390 | 0.923 |
| 1 | [12]C5 [13]C [1]H12 [16]O6 | 181.066745 | 0.060 |
| 2 | [12]C6 [1]H12 [16]O5 [18]O | 182.067644 | 0.011 |
| 3 | [12]C6 [1]H12 [16]O5 [17]O | 181.067607 | 0.002 |
| 4 | [12]C4 [13]C2 [1]H12 [16]O6 | 182.070100 | 0.002 |
| 5 | [12]C6 [1]H11 [2]H [16]O6 | 181.069667 | 0.001 |
| 6 | [12]C5 [13]C [1]H12 [16]O5 [18]O | 183.070999 | 0.001 |
| 7 | [12]C5 [13]C [1]H12 [16]O5 [17]O | 182.070962 | 0.000 |
The table lists the isotopologues in the order of descending abundance. for each isotopologue, isotope composition and exact mass, and corresponding abundances are list. The nominal isotopologue M1 is dominated by 13C and M2 is dominated by 18O.
In practice, most mass spectrometers can’t resolve the isotopologue fine spectrum and the degree of details of measured isotopologue patterns depends on instrumental mass resolution.
The method measured_centroids allows considering mass resolution of the instrument. The function is almost the same as compute_centroids with exception of the additional argument
R: resolution defined as as mz / FWHM (full peak width at half maximum in profile mode)
Some examples:
[5]:
measured = emzed.chemistry.measured_centroids
mf = "C6H12O6"
measured(mf, R=6e4, explained_abundance=0.999)
[5]:
| id | R | m0 | abundance |
|---|---|---|---|
| int | float | MzType | float |
| 0 | 60000.000000 | 180.063390 | 0.926 |
| 1 | 60000.000000 | 181.066774 | 0.062 |
| 2 | 60000.000000 | 182.067707 | 0.012 |
| 3 | 60000.000000 | 183.070999 | 0.001 |
At R = 60’000 nominal M1 isotopologues are no longer separated.
[6]:
measured(mf, R=6e4, explained_abundance=0.99999)
[6]:
| id | R | m0 | abundance |
|---|---|---|---|
| int | float | MzType | float |
| 0 | 60000.000000 | 180.063390 | 0.926 |
| 1 | 60000.000000 | 181.066774 | 0.062 |
| 2 | 60000.000000 | 182.067707 | 0.012 |
| 3 | 60000.000000 | 183.071038 | 0.001 |
| 4 | 60000.000000 | 184.072072 | 0.000 |
| 5 | 60000.000000 | 185.075253 | 0.000 |
When increasing explained_abundance we obtain also the very low nominal isotopologues M4 and M5. However, in most cases they are of low relevance but calculation time increases significantly. Along the same line, it is possible to calculate all possible isotopologeus by setting explained_abundance = 1 but it leads to a drastical increase in calculation time add most isotopologues are of extremely low abundance and cannot be measured anyway.
[7]:
measured(mf, R=2.4e5, explained_abundance=0.999)
[7]:
| id | R | m0 | abundance |
|---|---|---|---|
| int | float | MzType | float |
| 0 | 240000.000000 | 180.063390 | 0.925 |
| 1 | 240000.000000 | 181.066746 | 0.060 |
| 2 | 240000.000000 | 181.069667 | 0.001 |
| 3 | 240000.000000 | 182.067644 | 0.011 |
| 4 | 240000.000000 | 182.070102 | 0.002 |
| 5 | 240000.000000 | 183.070999 | 0.001 |
Increasing Resolution to 240’000 resolves 13C and 17O of M1, and 18O and a combination of some other low abundant nominal M2 isotopologues
[8]:
mf = "C6H12O6"
measured(
mf,
R=6e4,
explained_abundance=0.999,
abundances=dict(C={12: 0.02, 13: 0.98}),
)
[8]:
| id | R | m0 | abundance |
|---|---|---|---|
| int | float | MzType | float |
| 0 | 60000.000000 | 184.076810 | 0.005 |
| 1 | 60000.000000 | 185.080165 | 0.107 |
| 2 | 60000.000000 | 186.083521 | 0.873 |
| 3 | 60000.000000 | 187.084854 | 0.001 |
| 4 | 60000.000000 | 187.088181 | 0.002 |
| 5 | 60000.000000 | 188.087774 | 0.011 |
| 6 | 60000.000000 | 190.092028 | 0.000 |
We can also calculate the pattern for user defined abundances. Here the pattern would correspond to a 98% U-13C labeled glucose.
[9]:
mf = "[13]CC5H12O6"
measured(mf, R=6e4, explained_abundance=0.999)
[9]:
| id | R | m0 | abundance |
|---|---|---|---|
| int | float | MzType | float |
| 0 | 60000.000000 | 181.066745 | 0.935 |
| 1 | 60000.000000 | 182.070135 | 0.052 |
| 2 | 60000.000000 | 183.071041 | 0.012 |
| 3 | 60000.000000 | 184.074354 | 0.001 |
Finally, we can calculate the patterns of specific labeled compounds.
The method formula_table allows assigning potential molecular formulas to monoisotopic masses with the possibility to reduce the solution space. It is a Python version of the HR2 formula generator for CHNOPS applying filter heuristics for formula selection seven golden rules. The method is quite flexible and can be adapted to multiple use cases but results in many arguments.
formula_table(min_mass, max_mass, *, mass_c=12.0, mass_h=1.0078250319, mass_n=14.003074, mass_o=15.994915, mass_p=30.97376149, mass_s=31.97207073, c_range=None, h_range=None, n_range=None, o_range=None, p_range=None, s_range=None, apply_rules=True, apply_rule_1=True, apply_rule_2=True, apply_rule_4=True, apply_rule_5=True, apply_rule_6=True, rule_45_range='extended')
However, most arguments are optional and only min_mass and max_mass are required. By default all seven heuristic filters will be applied. An example
[10]:
formula_table = emzed.chemistry.formula_table
m0 = emzed.mass.of("C6H12O6")
min_mass = m0 - 0.003
max_mass = m0 + 0.003
formula_table(min_mass, max_mass)
[10]:
| mf | m0 |
|---|---|
| str | MzType |
| C2H8N6O4 | 180.060704 |
| C10H12OS | 180.060886 |
| C3H4N10 | 180.062040 |
| C6H12O6 | 180.063390 |
| C7H16OS2 | 180.064257 |
| C7H8N4O2 | 180.064726 |
| H8N10S | 180.065411 |
| C5H13N2O3P | 180.066380 |
In total, the resulting table contains 8 molecular formulas including the correct one of glucose, when switching of the seven golden rules we obtain
[11]:
len(formula_table(min_mass, max_mass, apply_rules=False))
[11]:
25
Hence, we otain about 3 times more possible solutions. In general, it is helpful to use all available information for solution space restriction. For instance, if the M2 isotopologue was measured with a high mass resolution instrument, one can easily check for presence of sulfur assuming a CHNOPS elemental composition:
[12]:
emzed.abundance.S
[12]:
{32: 0.9493, 33: 0.0076, 34: 0.0429, 36: 0.0002}
[13]:
emzed.mass.S34 - emzed.mass.S32
[13]:
1.9957962699999996
[14]:
emzed.abundance.O
[14]:
{16: 0.9975700000000001, 17: 0.00037999999999999997, 18: 0.0020499999999999997}
[15]:
emzed.mass.O18 - emzed.mass.O16
[15]:
2.0042539999999978
In other words, if I can measure the M2 isotopologue of a low weight compound and I do not observe mass difference of about 1.996, S can be excluded from the molecular formula end we would end up with
[16]:
formula_table(min_mass, max_mass, s_range=(0, 0))
[16]:
| mf | m0 |
|---|---|
| str | MzType |
| C2H8N6O4 | 180.060704 |
| C3H4N10 | 180.062040 |
| C6H12O6 | 180.063390 |
| C7H8N4O2 | 180.064726 |
| C5H13N2O3P | 180.066380 |
Finaly molecular formulas can also be assigned to labeled compounds.
[17]:
m0 = emzed.mass.of("[13]C6H12O6")
min_mass = m0 - 0.003
max_mass = m0 + 0.003
mass_c = emzed.mass.C13
formula_table(min_mass, max_mass, mass_c=mass_c)
[17]:
| mf | m0 |
|---|---|
| str | MzType |
| C10H8O3 | 186.080895 |
| H10N8O4 | 186.082502 |
| C6H12O6 | 186.083520 |
You can transform string presentations of molecular formulas into MolecularFormula objects (MF). Molecular formulas can handle typical formula representation i.e. structuring formulas by functional groups i.e. CH3(CH2)2COOH. Morever, additon and subtraction of MF objects is supported. Two examples
[18]:
mf = emzed.mf
gluc = mf("(CH2O)6")
h2o = mf("H2O")
res = gluc - h2o
res.as_string()
[18]:
'C6H10O5'
[19]:
so4 = mf("SO4")
gluc - so4
[19]:
<MolecularFormula '<invalid>'>
Whereas the first example yields the correct result, the second operation is obviously not possible since ‘gluc’ contains no sulfur and causes an error.
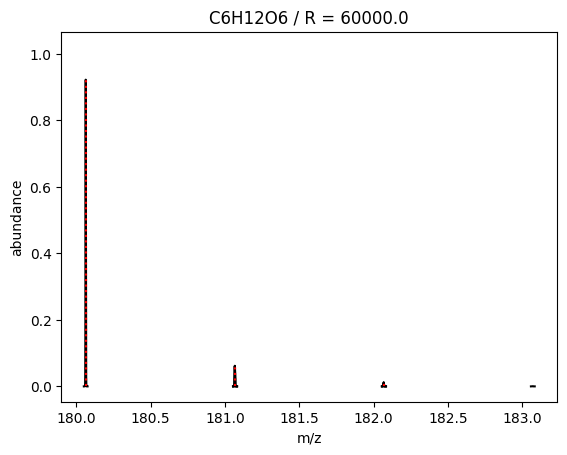
Finally, the method plot_profile plots isotopologue patterns of molecular formulas. Its usage is very similar to measured_centroids and shares the same method arguments except the one additional argument
path: path to save plot to. If not provided a plot window will pop up.
An example:
[20]:
# define the target path
plot_profile = emzed.chemistry.plot_profile
plot_profile("C6H12O6", R=6e4, explained_abundance=0.999)
© Copyright 2012-2025 ETH Zurich
Last build 2025-10-28 13:23:38.200852.
Created using Sphinx 8.1.3.